廣義線性回歸模型之型式

屬性解釋變數

資料可以分成屬性資料（Qualitative Data）與屬量資料（Quantitative Data），前者資料是基於類別或排序，包含：名目尺度、順序尺度；而後者資料為可衡量或可測量的數值，包含：區間尺度、比例尺度。而廣義線性回歸的解釋變數不只可以放屬量資料，也可以放屬性資料，或兩者混放。

以前面介紹的兩解釋變數之一階模型為例，其中解釋變數 X1 放屬量資料「年紀」；X2 放屬性資料「性別」。於此，可以虛擬變數（dummy variable）的方式定義

而回歸模型為

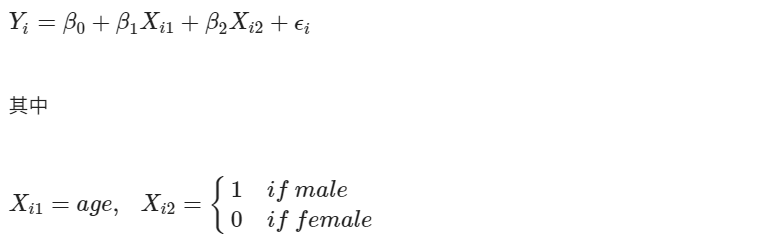
若想要觀察男性對模型的影響，取 X2 = 1，則

反之，若想要觀察女性對模型的影響，取 X2 = 0，則

不同性別在截距項相差 Beta2 。所以加廣型線性回歸解釋變數可為屬性或屬量之樣態。

線性模型的涵義

前文提到線性回歸的線性係指參數的線性。所以線性不是指在反應曲面（response surface）的線性或解釋變數的線性。以下說明原屬線性的回歸模型在加入交互作用項、高次方的解釋變數或對變數做轉換之後，只要沒有動到參數，仍屬線性。最終，導引出線性回歸模型的一般樣式，

交互作用項

線性回歸模型加入交互作用項後仍屬加廣型線性回歸模型。例如模型

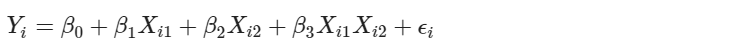
其中 Xi1 * Xi2 為交互作用項。我們可以把交互作用項用另一個新設的變數替換掉，如設 Xi3 = Xi1 * Xi2，則模型可改寫成

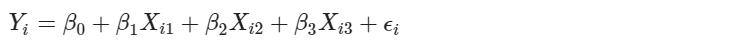
其符合加廣型線性回歸的型式。

高次方的解釋變數

將解釋變數換成高次方後，仍屬加廣型線性回歸模型。例如模型

利用同樣的方式在再做一次，設 Xi3 = Xi2^3，也可將模型改寫為加廣型線性回歸模型的型式。

轉換變數

將解釋變數做轉換後，仍屬加廣型線性回歸模型。例如對反應變數取自然對數

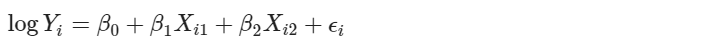
可以設新的反應變數 Yi' 取代原先的反應變數 log(Yi)，則模型改寫成

為加廣型線性回歸模型的型式。

小結

只要變數經替換後可以轉變成廣義線性回歸模型之型式，就還是線性回歸模型。本文利用許多例子說明參數上線性的涵義，包含：交互作用、高次的解釋變數、轉換變數。一些乍看之下不屬線性的回歸模型，其實還是滿足所謂「參數上的線性（linear in parameters）」的定義。據此，將案例歸納成以下結論：只要回歸模型可以表示為

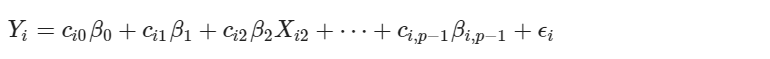
的型式，符合參數的線性，則該回歸模型為線性。

參考資料

本文都在介紹線性回歸模型，但也有一些回歸模型為非線性，例如：Logistic Regression、Exponential Regression、Poisson Regression 等。若想進一步瞭解非線性回歸模型，可參見：Pennsylvania State University 的 Applied Regression Analysis 課程網站。

另外，在閱讀參考資料中的回歸專業書籍（Applied Linear Statistical Models, page.547）時，讀到非線性模型的章節，注意到一張表格，如下所示，其為統計與神經網路的專業名詞對照表（取自書中，由筆者重新畫表）。覺得該表蠻有趣的，跟大家分享！

**************************** 統計與神經網路之專業名詞對照表 ****************************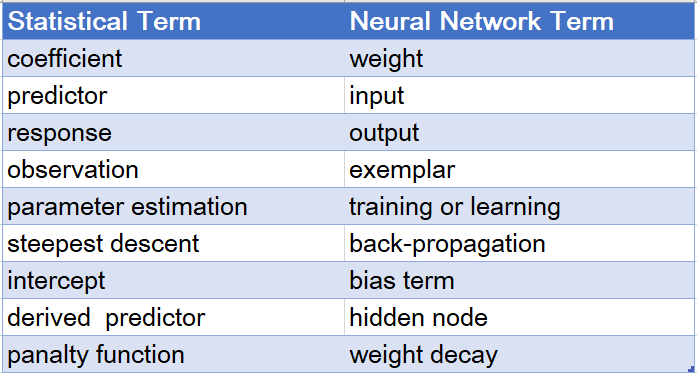

書籍資料：

• Michael H. Kutner, Christopher J. Nachtsheim, John Neter, and William Li (2019), Applied Linear Statistical Models. McGraw Hill, New York.